
Sub-module 3A, Page 6
The reason is that the MEK concentration of water you are removing for those 10 hours is not 100 mg/ L. At every instant, you are removing some mass from the lake and the concentration left in the lake is constantly decreasing. That is, you are removing a constantly smaller amount of contaminant with each succeeding time increment.
Lets look at a finite increment of time,

You may remember from calculus, that when you make the time increment delta t small enough (infinitely small), you call it dt. And you wrote a differential equation that looked like:

Where "e" is the base of the natural logarithms. Or your teacher may have used a different example, perhaps radioactive decay or what ever, but the final form looked the same. Except the the Q over V term was replaced by a "k." This k is known by many names, rate constant, time constant, etc., but its units are always one over time. In our example, the k would be
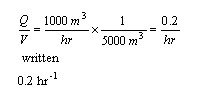
So now it is simple to write an expression for the concentration of MEK in the lake. It is
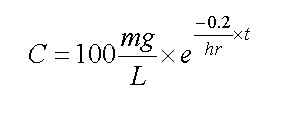
Where the initial concentration was 100 mg / L. All you need is a hand held calculator and the time since the spill and you can calculate the concentration. [HW problem #3]